第 14 章 强化学习
强化学习(Reinforcement Learning,RL)是一种实现通用人工智能的可能方法。之前我们学习过监督学习,可先从监督学习与强化学习的关系来理解强化学习。图 14.1 是监督学习(supervised learning)的示例,假设我们要训练一个图像的分类器,给定机器一个输入,要告诉机器对应的输出。目前为止,本书所提及的方法都是基于监督学习的方法。自监督学习只是标签,不需要特别雇用人力去标记,它可以自动产生。即使是无监督的方法,比如自编码器(Auto-Encoder,AE),其没有用到人类的标记。但事实上还有一个标签,只是该标签的产生不需要耗费人类的力量。
图 14.1 监督学习
但在强化学习里面,给定机器一个输入,最佳的输出也是未知的。如图 14.2 所示,假设要让机器学习下围棋,如果使用监督学习的方法,我们需要告诉机器,给定一个盘势,下一步落子的最佳位置,但该位置也是未知的。即使让机器阅读很多职业高段棋士的棋谱,这些棋谱里面给定某一个盘势,人类下的下一步。但这是一个很好的答案,不一定是最好的位置,因此正确答案是未知的。当正确答案是未知的或者收集有标注的数据很困难,我们可以考虑使用强化学习。强化学习在学习的时候,机器不是一无所知的,虽然其不知道正确的答案,但会跟环境(environment)互动得到奖励(reward),所以其会知道其输出的好坏。通过与环境的互动,机器可以知道输出的好坏,从而学出一个模型。
图 14.2 强化学习
如图 14.3 所示,强化学习里面有一个智能体(agent)和一个环境,智能体会跟环境互动。环境会给智能体一个观测(observation,),智能体看到这个观测后,它会采取一个动作。该动作会影响环境,环境会给出新的观测,智能体会给出新的动作。
观测是智能体的输入,动作是智能体的输出,所以智能体本身就是一个函数。这个函数的输入是环境给它的观测,输出是智能体要采取的动作。在互动的过程中,环境会不断地给智能体奖励,让智能体知道它现在采取的这个动作的好坏。智能体的目标是要最大化从环境获得的奖励总和。
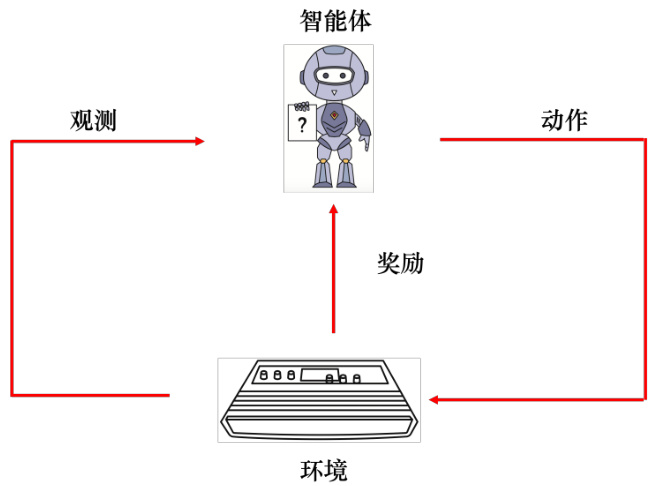
图 14.3 强化学习示意
14.1 强化学习应用
强化学习有很多的应用,比如玩视频游戏、下围棋等等。
14.1.1 玩电子游戏
强化学习可以用来玩游戏,强化学习最早的几篇论文都是让机器玩《太空侵略者》。在《太空侵略者》里面,如图 14.4 所示,我们要操控太空梭来杀死外星人,可采取的动作有三个:左移、右移和开火,开火击中外星人,外星人就死掉了,我们就得到分数。我们可以躲在防护罩后面来挡住外星人的攻击,如果不小心打到防护罩,防护罩就会消失。在某些版本的《太空侵略者》里面,会有补给包,如果击中补给包,会被加一个很高的分数。分数其实环境给的奖励。当所有的外星人被杀光或者外星人击中母舰的时候,游戏就会终止。
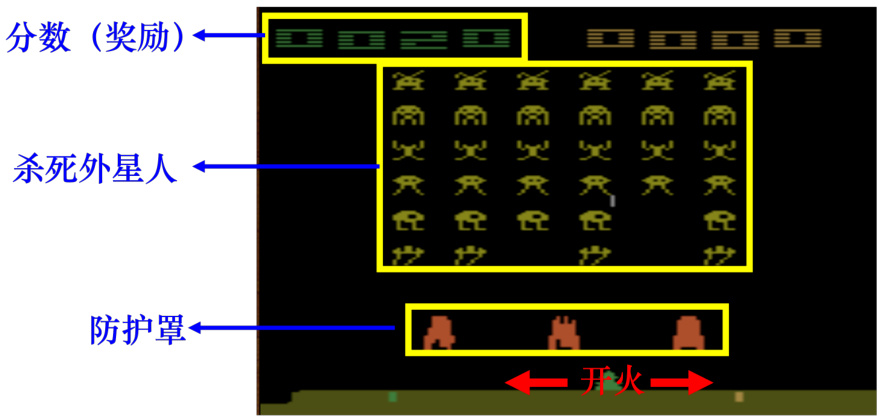
图 14.4 《太空侵略者》游戏
如果用强化学习玩《太空侵略者》,如图 14.5 所示。智能体会去操控摇杆,控制母舰来和外星人对抗。环境是游戏主机,游戏主机操控外星人攻击母舰,所以观测是游戏的画面。输入智能体一个游戏的画面,输出是智能体可以采取的动作。当智能体采取右移动作的时候,不可能杀掉外星人,所以奖励为 0。智能体体采取一个动作后,游戏的画面就变了,也就有了新的观测。根据新的观测,智能体会决定采取新的动作。假设如图 14.6 所示,智能体采取的动作是开火,这个动作正好杀掉了一只外星人,得到 5 分,奖励等于 5。在玩游戏的过程中,智能体会不断地采取动作得到奖励,我们想要智能体玩这个游戏得到的奖励的总和最大。
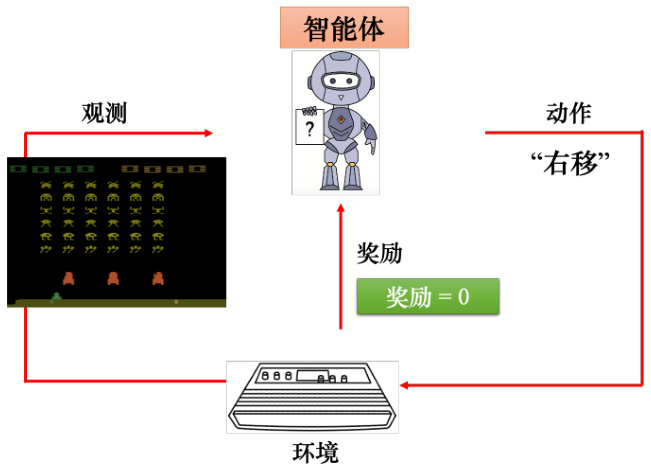
图 14.5 智能体玩《太空侵略者》采取右移的动作
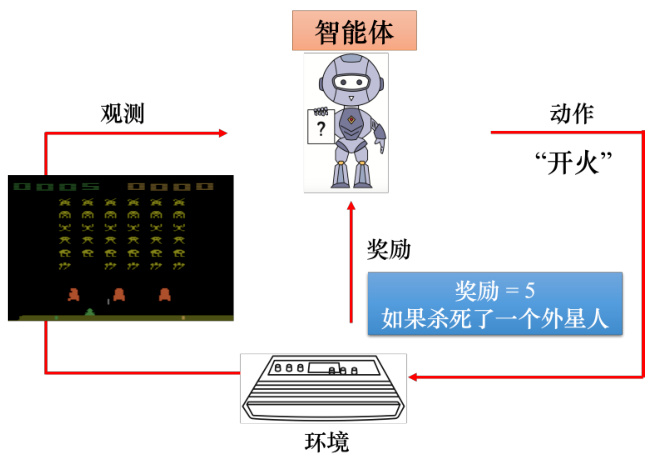
图 14.6 智能体玩《太空侵略者》采取开火的动作
14.1.2 下围棋
如果用强化学习下围棋,如图 14.7(a) 所示,智能体是 AlphaGo,环境是 AlphaGo 的人类对手,即棋士。智能体的输入是棋盘上黑子跟白子的位置。一开始,棋盘上是空的。根据该棋盘,智能体要决定下一步的落子,有
如图 14.7(b) 所示,假设现在智能体决定了落子。新的棋盘会输入给棋士,棋士棋士也会再落一子,产生新的观测。智能体看到新的观测就会产生新的动作,这个过程反复进行。在下围棋里面,智能体所采取的动作都无法得到任何奖励,我们可以定义,如果赢了,就得到 1分,如果输了就得到 -1 分,只有整场围棋结束,智能体才能够拿到奖励。智能体学习的目标是要最大化它可能得到的奖励。
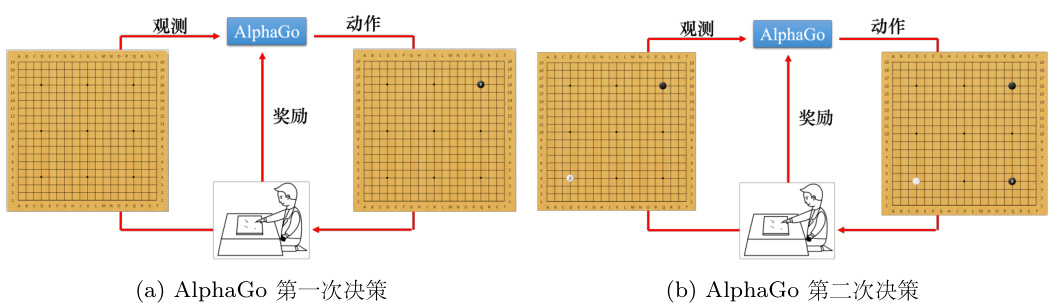
图 14.7 强化学习下围棋
Q:下围棋是否需要比较好的启发式函数?
A: 在下围棋的时候,假设奖励非常地稀疏(sparse),我们可能会需要一个好的启发式函数(heuristic function),深蓝的那篇论文,深蓝其实已经在西洋棋上打爆人类了,深蓝就有蛮多启发式函数,它就不是只有下到游戏的中盘,才知道才得到奖励,中间会有蛮多的状况它都会得到奖励。
14.2 强化学习框架
强化学习跟机器学习的框架类似,机器学习有三个步骤:第一步是定义函数,函数里面有一些未知变量,这些未知变量是要被学出来的;第二步是定义损失函数;最后一步是优化,即找出未知变量去最小化损失。强化学习也是类似的三个步骤。
14.2.1 第 1 步:未知函数
第一个步骤,有未知数的函数是智能体。在强化学习里面,智能体是一个网络,通常称为策略网络(policy network)。在深度学习未被用到强化学习的时候,通常智能体是比较简单的,其不是网络,它可能只是一个查找表(look-up table),告诉我们给定输入对应的最佳输出。网络是一个很复杂的函数,其输入是游戏画面上的像素,输出是每一个可以采取的动作的分数。
网络的架构可以自己设计,只要网络能够输入游戏的画面,输出动作。比如如果输入是张图片,可以用卷积神经网络来处理。如果我们不要只看当前这一个时间点的游戏画面,而是要看整场游戏到目前为止发生的所有画面,可以考虑使用循环神经网络或Transformer。
如图 14.8 所示,输入游戏画面,策略网络的输出是左移 0.7 分、右移 0.2 分、开火 0.1分。这类似于分类网络,分类是输入一张图片,输出是决定这张图片的类别,网络会给每一个类别一个分数。分类网络的最后一层是 softmax 层,每个类别有个分数,这些分数的总和是1。机器会决定采取哪一个动作,取决于每一个动作的分数。常见的做法是把这个分数当做一个概率,按照概率采样,随机决定要采取的动作。比如图 14.8 中的例子里面,智能体有
Q:为什么不采取分数最大的动作?
A:我们可以采取左的动作,但一般都是使用随机采样。采取有一个好处:看到同样的游戏画面,机器每一次采取的动作,也会略有不同,在很多的游戏里面随机性是很重要的,比如玩石头、剪刀、布游戏,如果智能体总是出石头,很容易输。但如果有一些随机性,就比较不容易输。
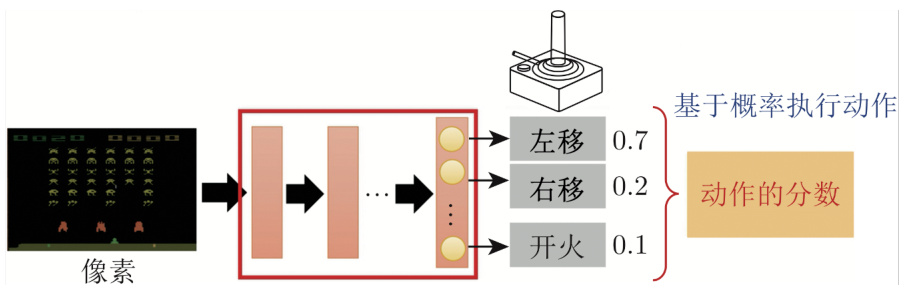
图 14.8 策略网络
14.2.2 第 2 步:定义损失
接下来第二步是定义强化学习中的损失。如图 14.9 所示,首先有一个初始的游戏画面
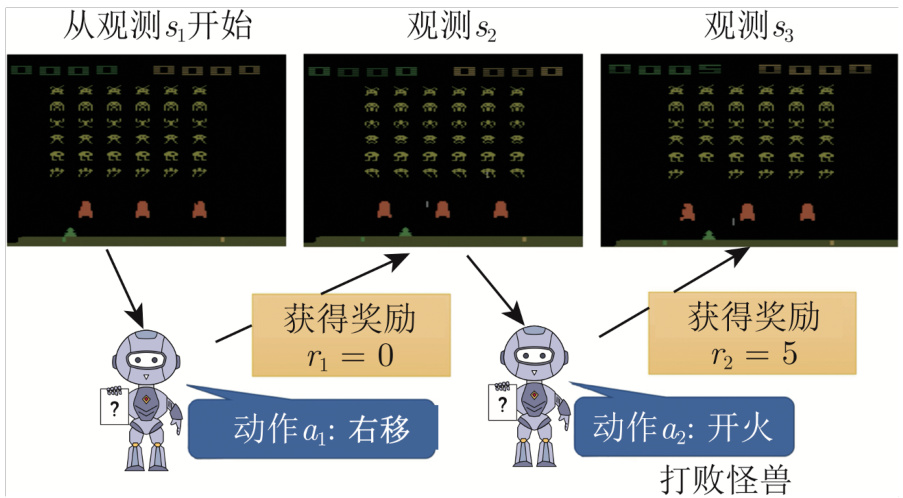
图 14.9 玩视频游戏的例子
智能体采取开火这个动作以后,接下来会有新的游戏画面,机器又会采取新的动作,这个互动的过程会反复持续下去,直到机器在采取某一个动作以后,游戏结束了。从游戏开始到结束的整个过程称为一个回合(episode)。整个游戏过程中,机器会采取非常多的动作,每一个动作会有奖励,所有的奖励的总和称为整场游戏的总奖励(total reward),也称为回报(return)。回报是从游戏一开始得到的
奖励是指智能体采取某个动作的时候,立即得到的反馈。整场游戏里面所有奖励的总和才是回报。
14.2.3 第 3 步:优化
图 14.10 给出了智能体与环境互动的示例,环境输出一个观测
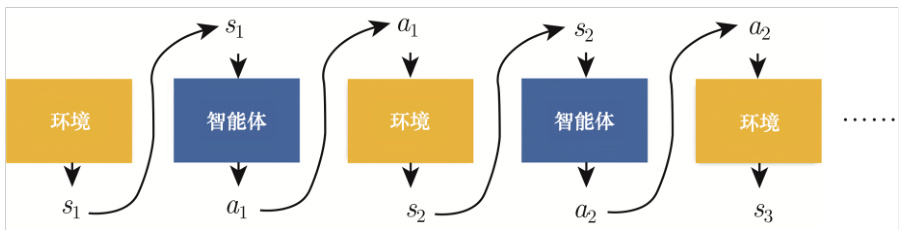
图 14.10 智能体与环境互动
如图 14.11 所示,智能体与环境互动的过程中,会得到奖励,奖励可以看成一个函数。奖励函数有不同的表示方法,在有的游戏里面,智能体采取的动作可以决定奖励。但通常我们在决定奖励的时候,需要动作和观测。比如每次开火不一定能得到分数,外星人在母舰前面,开火要击到外星人才有分数。因此通常定义奖励函数的时候,需要同时看动作跟观测,因此奖励函数的输入是状态和动作。比如图 14.11 中奖励函数的输入是
我们需要最大化回报,因此优化问题为:学习网络的参数让回报越大越好,可以通过梯度上升(gradient ascent)来最大化回报。但是强化学习困难的地方是,这不是一般的优化的问题,跟一般的网络训练不太一样。第一个问题是,智能体的输出是有随机性的,比如图 14.11 中的
另外一个问题是环境跟奖励是一个黑盒子,其很有可能具有随机性。比如环境是游戏机,游戏机里面发生的事情是未知的。在游戏里面,通常奖励是一条规则:给定一个观测和动作,输出对应的奖励。但对有一些强化学习的问题里面,奖励是有可能有随机性的,比如玩游戏也是有随机性的。给定同样的动作,游戏机的回应不一定是一样的。如果是下围棋,即使智能体落子的位置是相同的,对手的回应每次可能也是不一样的。由于环境和奖励的随机性,强化学习的优化问题不是一般的优化的问题。
强化学习的问题是如何找到一组网络参数来最大化回报。这跟生成对抗网络有异曲同工之妙。在训练生成器(generator)的时候,生成器与判别器(discriminator)会接在一起,我们希望调整生成器的参数,让判别器的输出越大越好。在强化学习里面,智能体就像是生成器,环境跟奖励就像是判别器,我们要调整生成器的参数,让判别器的输出越大越好。但在生成对抗网络里面判别器也是一个神经网络,我可以用梯度下降来训练生成器,让判别器得到最大的输出。但是在强化学习的问题里面,奖励跟环境不是网络,不能用一般梯度下降的方法调整参数来得到最大的输出,所以这是强化学习跟一般机器学习不一样的地方。
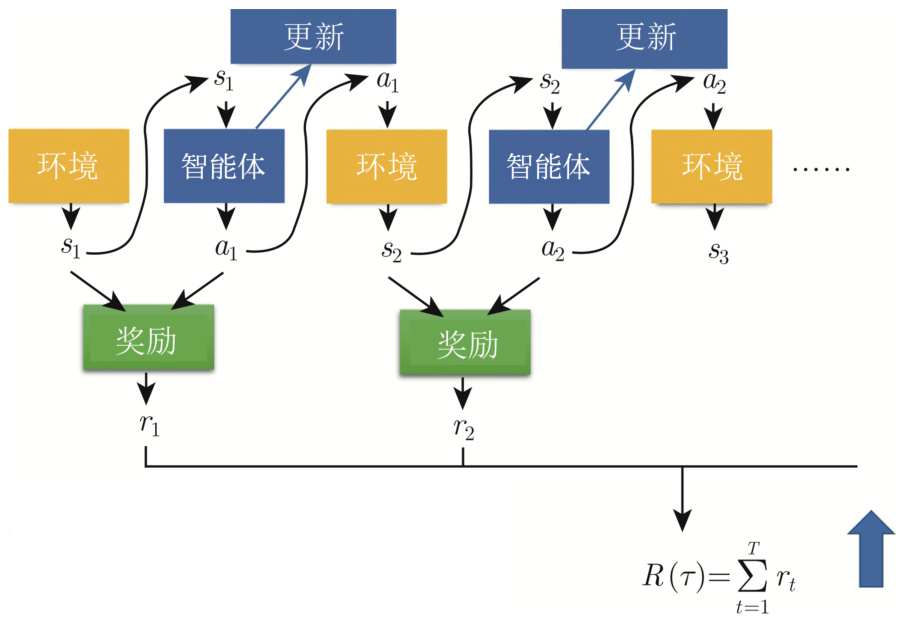
图 14.11 期望的奖励
让一个智能体在看到某一个特定观测的时候,采取某一个特定的动作,这可以看成一个分类的问题,如图 14.12 所示,比如给定智能体的输入是
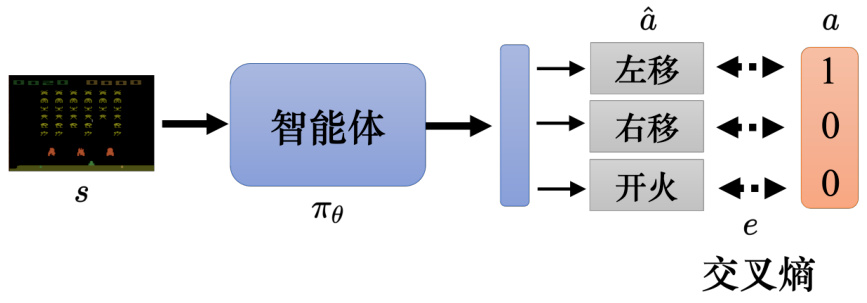
图 14.12 使用交叉熵作为损失
如果想要让智能体看到某一个观测,不要采取某一个动作,只需要在定义损失的时候使用负的交叉熵。如果希望智能体采取动作
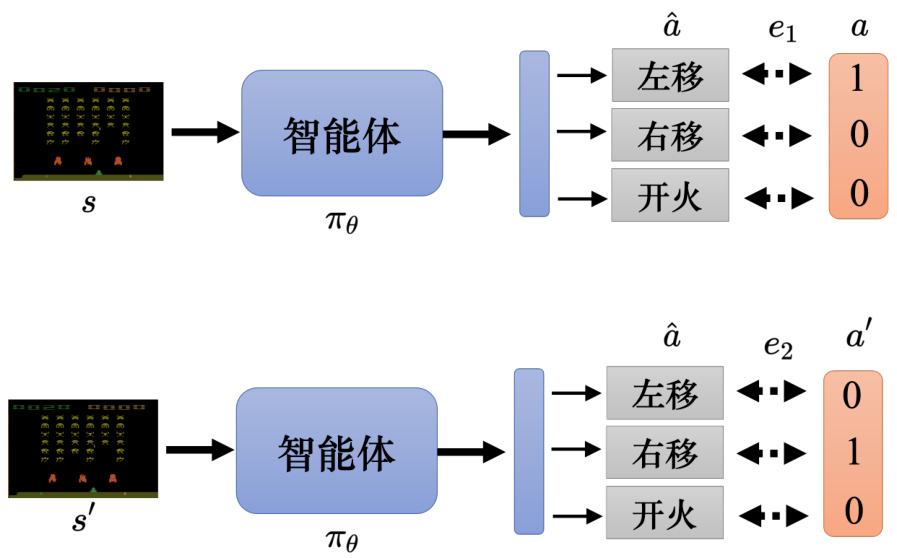
图 14.13 定义合适的损失
如图 14.14 所示,如果我们要训练一个智能体,需要收集一些训练数据,希望在
接着最小化损失函数,这样我们可以训练一个智能体,期待它执行的动作是我们想要的。而且可以更进一步,每一个动作并不是有想要执行跟不想要执行,而且有程度的差别。如果每一个动作就是要执行或不执行,这是一个二分类的问题,可以用

图 14.14 收集训练数据
但如果考虑动作执行程度的差别,每一个状态-动作对(state-action pair)对应一个分数,这个分数代表希望机器在看到
训练数据

图 14.15 对每个状态-动作对分配不同的分数
综上,强化学习可分为三个阶段,只是在优化的步骤跟一般的方法不同,其会使用策略梯度(policy gradient)等优化方法。接下来的难点就是,如何定义
14.3 评价动作的标准
本节介绍下评价动作的多种标准。
14.3.1 使用即时奖励作为评价标准
智能体跟环境做互动可以收集一些训练数据(状态-动作对)。智能体可以先看成随机的智能体,它执行的动作都是随机的,每一个
以上是版本 0,但其并不是一个好的版本。因为把奖励设为
而且在跟环境做互动的时候,有一个问题叫做延迟奖励(delayed reward),即牺牲短期的利益以换取更长期的利益。比如在《太空侵略者》的游戏里面,智能体要先左右移动一下进行瞄准,射击才会得到分数。而左右移动是没有任何奖励的,其得到的奖励是零。只有射击才会得到奖励,但是并不代表左右移动是不重要的,先需要左右移动进行瞄准,射击才会有效果,所以有时候我们会牺牲一些近期的奖励,而换取更长期的奖励。如果使用版本 0,左移和右移的奖励为 0,开火的奖励为正,智能体会觉得只有开火是对的,它会一直开火。
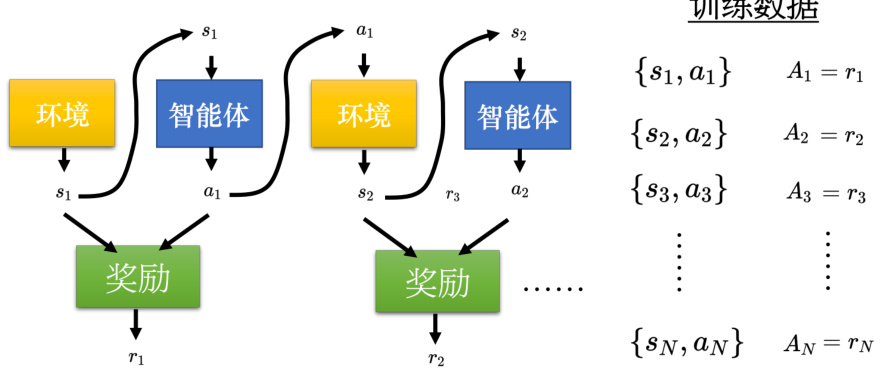
图 14.16 短视的版本
14.3.2 使用累积奖励作为评价标准
在版本 1 里面,把未来所有的奖励加起来即可得到累积奖励
比如
但是版本 1 也有问题,假设游戏非常长,把
14.3.3 使用折扣累积奖励作为评价标准
版本 2 的累积的奖励用
训练数据
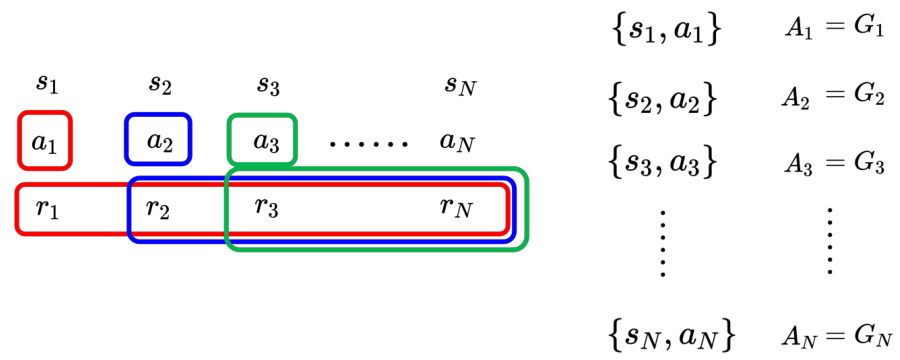
图 14.17 使用累积奖励作为评价标准
图 14.18 给出了折扣累积奖励的示例,
距离采取动作
训练数据
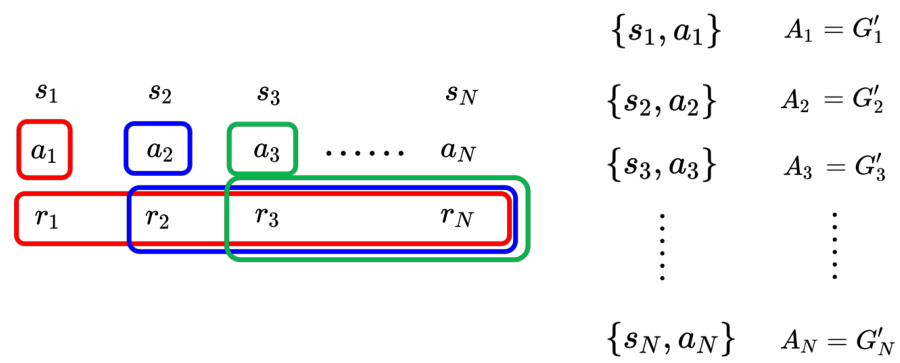
图 14.18 使用折扣奖励作为评价标准
所以加入折扣因子可以把给离
Q:越早的动作累积到的分数越多,越晚的动作累积的分数越少吗?A:在游戏等情况里,越早的动作就会累积到越多的分数,因为较早的动作对接下来的影响比较大,其是需要特别在意的。到游戏的终局,外星人基本都没了,智能体做的事情对结果影响都不大。有很多种不同的方法决定
Q:折扣累积奖励是不是不适合用在围棋之类的游戏(围棋这种游戏只有结尾才有分数)?
A:折扣累积奖励可以处理这种结尾才有分数的游戏。假设只有
14.3.4 使用折扣累积奖励减去基线作为评价标准
因为好或坏是相对的,假设在游戏里面,我们每次采取一个行动的时候,最低分预设是10 分,其实得到 10 分的奖励算是差的,奖励是相对的。用
训练数据
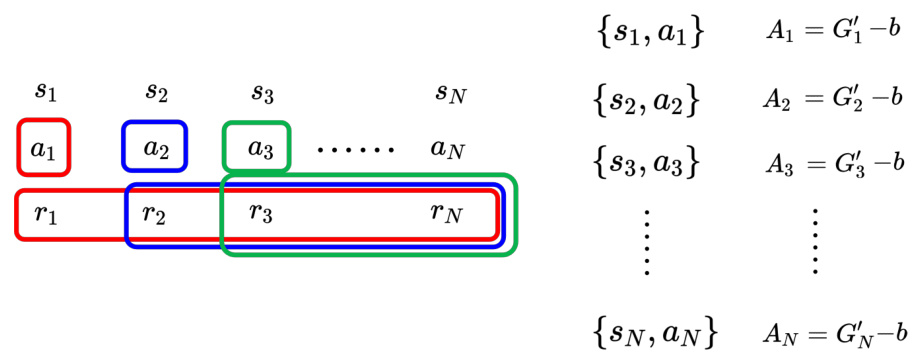
图 14.19 减去基线
策略梯度算法中的评价标准就是
算法 14.1 策略梯度
1 初始化智能体网络参数
2 for
3 使用智能体
4 获取数据
5 计算
6 计算损失
7
8 end
在一般的训练中,收集数据都是在训练迭代之外,比如有一堆数据,用这堆数据拿来做训练,更新模型很多次,最后得到一个收敛的参数,拿这个参数来做测试。但在强化学习不同,其在训练迭代的过程中收集数据。
如图 14.20 所示,可以用一个图像化的方式来表示强化学习训练的过程。训练数据中有很多某个智能体的状态-动作对,对于每个状态-动作对,可以使用评价
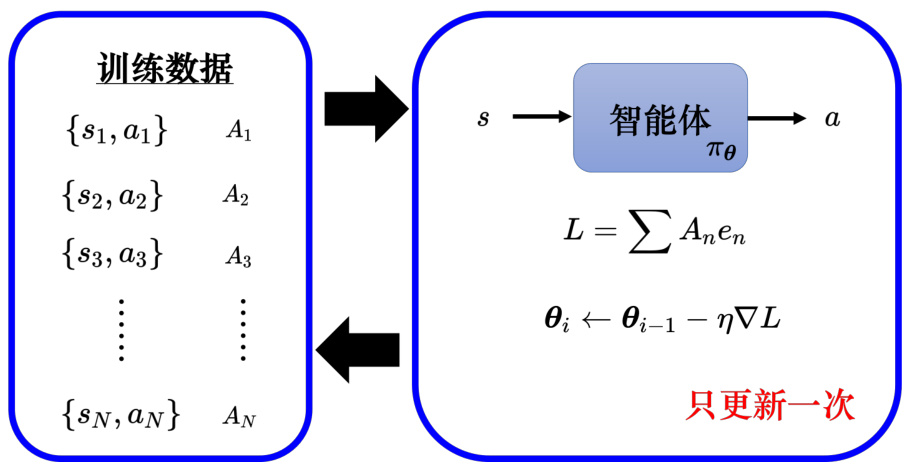
图 14.20 强化学习训练过程
策略梯度算法中,每次更新完模型参数以后,需要重新再收集数据。如算法 14.1 所示,这些数据是由
举个例子,进藤光跟佐为下棋,进藤光下了小马步飞(棋子斜放一格叫做小马步飞,斜放好几格叫做大马步飞)。下完棋以后,佐为让进藤光这种情况不要下小马步飞,而是要下大马步飞。如果大马步飞有 100 手,小马步飞只有 99 手。之前走小马步飞是对的,因为小马步飞的后续比较容易预测,也比较不容易出错,大马步飞的下法会比较复杂。但进藤光假设想要变强的话,他应该要学习下大马步飞,或者是进藤光变得比较强以后,他应该要下大马步飞。同样是下小马步飞,对不同棋力的棋士来说,其作用是不一样的。对于比较弱的进藤光,下小马
步飞是对的,因为这样比较不容易出错,但对于已经变强的进藤光来说,下大马步飞比较好。
因此同一个动作,对于不同的智能体而言,它的好是不一样的。
如图 14.21 所示,假设用
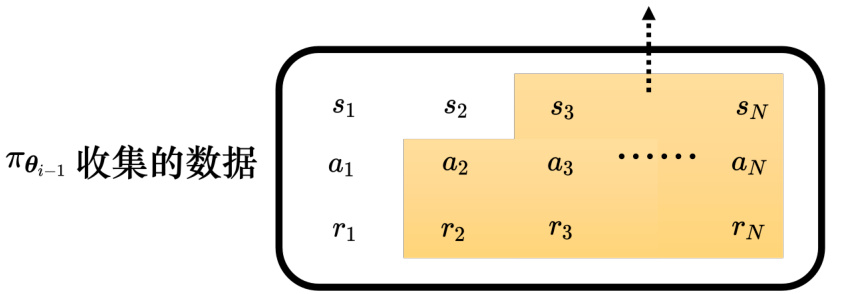
图 14.21 不同智能体收集的数据不能共用
同策略学习(on-policy learning)是指要训练的智能体跟与环境互动的智能体是同一个智能体,比如策略梯度算法就是同策略的学习算法。而在异策略学习中,与跟环境互动的智能体跟训练的智能体是两个智能体,要训练的智能体能够根据另一个智能体与环境互动的经验进行学习,因此异策略学习不需要一直收集数据。同策略学习每更新一次参数就要收集一次数据,比如更新 400 次参数,就要收集 400 次数据,而异策略学习收集一次数据,可以更新参数很多次。
探索(exploration)是强化学习训练的过程中一个非常重要的技巧。智能体在采取动作的时候是有一些随机性的。随机性非常重要,很多时候随机性不够会训练不起来。假设有一些动作从来没被执行过,这些动作的好坏是未知的,很有可能会训练不出好的结果。比如假设一开始初始的智能体永远都只会右移移动,它从来没有开火,动作开火的好坏就是未知的。只有某一个智能体试图做开火这件事得到奖励,才有办法去评估这个动作的好坏。在训练的过程中,与环境互动的智能体本身的随机性是非常重要的,其随机性大一点,才能够收集到比较多的数据,才不会有一些状况的奖励是未知的。
为了要让智能体的随机性大一点,甚至在训练的时候会刻意加大它的随机性。比如智能体的输出是一个分布,可以加大该分布的熵(entropy),让其在训练的时候,比较容易采样到概率比较低的动作。或者会直接在这个智能体的参数上面加噪声,让它每一次采取的动作都不一样。
14.3.5 Actor-Critic
与环境交互的网络可称为 Actor(演员,策略网络),而 Critic(评论员,价值网络)的工作是要来评估一个智能体的好坏。版本 3.5 跟 Critic 及其训练方法相关。假设有一个智能体的参数为
Critic 也被称为价值函数(value funciton),可以用
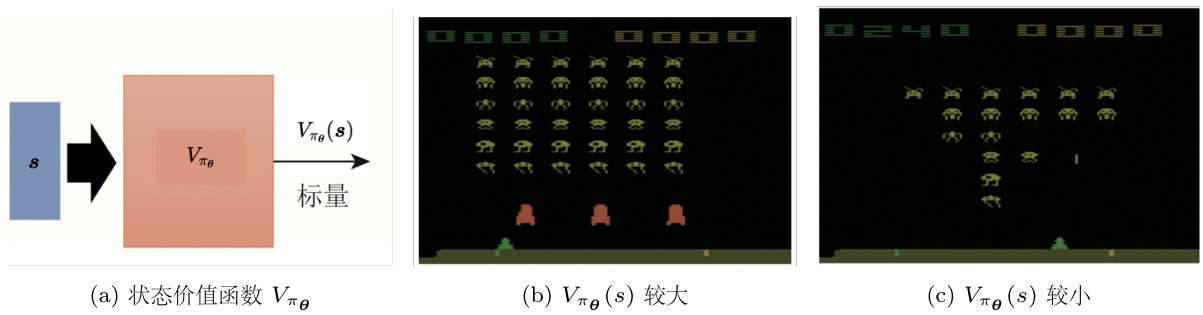
图 14.22 玩《太空侵略者》
Critic 有两种常用的训练方法:蒙特卡洛和时序差分。智能体跟环境互动很多轮会得到一些游戏的记录。从这些游戏记录可知,看到游戏画面
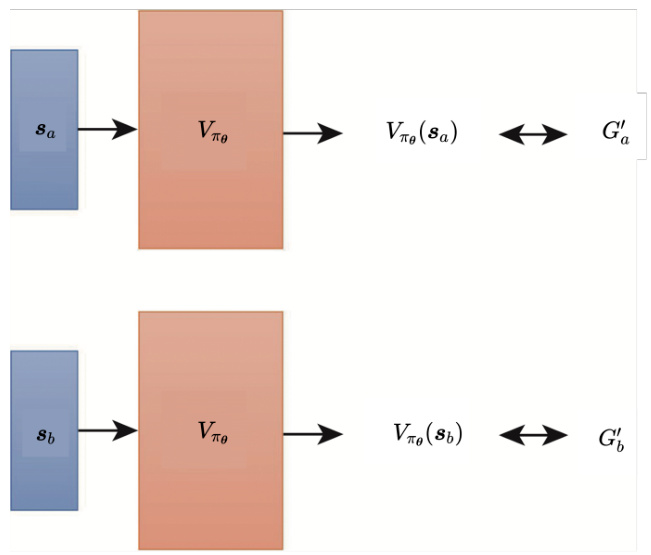
图 14.23 基于蒙特卡洛的方法
时序差分(Temporal-Diference,TD)方法不用玩完整场游戏,只要看到数据
假设有一笔数据为
同样的

图 14.24 时序差分方法与蒙特卡洛方法的差别[1]
为了简化计算,假设这些游戏都非常简单,一到两个回合就结束了。比如智能体第一次玩游戏的时候,它先看到画面
Q:如果
A:如果
为了简化起见,先忽略动作,并假设
因此
蒙特卡洛跟时序差分得出的结果都是对的,它们只是背后的假设是不同的。对蒙特卡洛而言,它就是直接看我们观察到的数据,
接下来介绍下如何用 Critic 训练 Actor。智能体跟环境互动得到一堆如图 14.25 所示的状态-动作对。比如
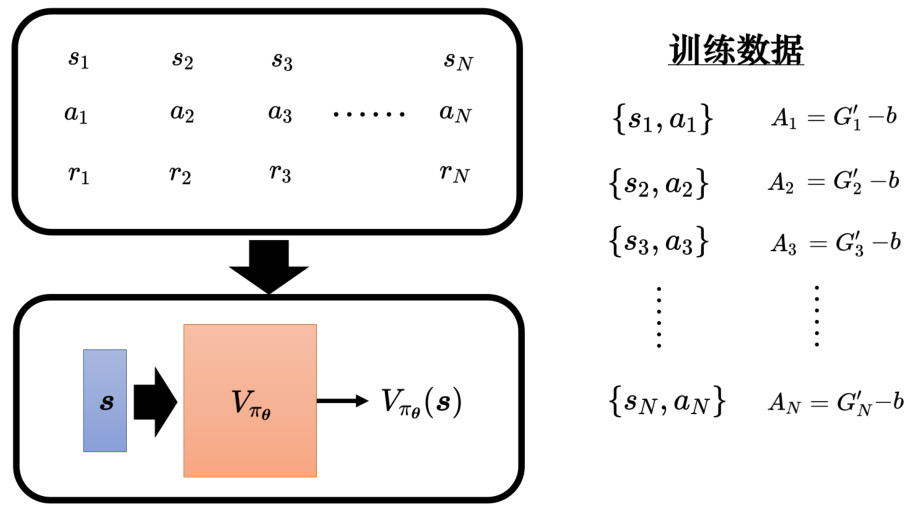
图 14.25 使用折扣累积奖励减去基线作为评价标准
学习出 Critic
训练数据
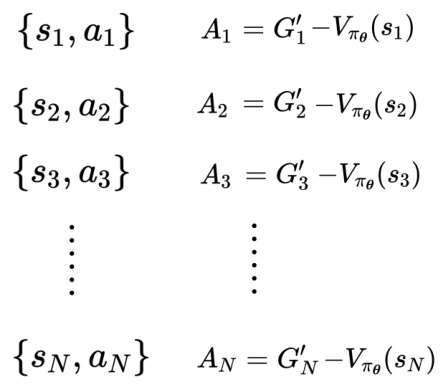
图 14.26 使用
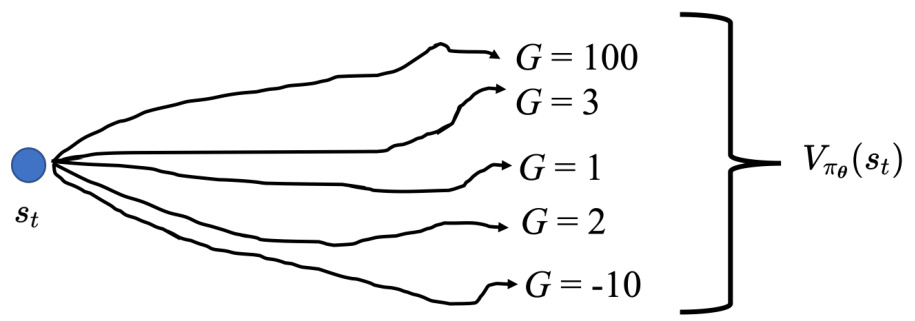
图 14.27 看到
把这些可能的结果平均起来,就是
接下来我们还可以做一个改进。
14.3.6 优势 Actor-Critic
执行完
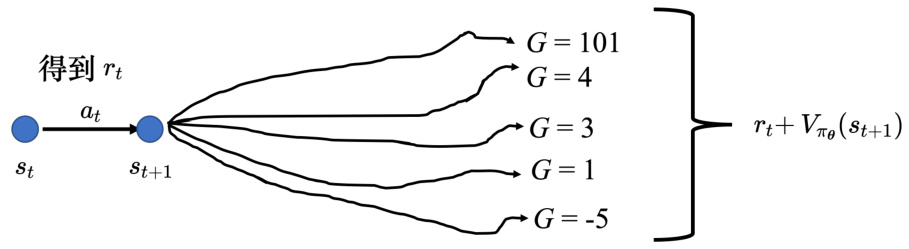
图 14.28 优势 Actor-Critic
Actor-Critic 有一个训练的技巧。Actor 和 Critic 都是一个网络,Actor 网络的输入是一个游戏画面,其输出是每一个动作的分数。Critic 的输入是游戏画面,输出是一个数值,代表接下来会得到的累积奖励。图 14.29 中有两个网络,它们的输入是一样的东西,所以这两个网络应该有部分的参数可以共用,尤其假设输入又是一个非常复杂的东西,比如说游戏画面,前面几层应该都需要是卷积神经网络。所以 Actor 和 Critic 可以共用前面几个层,所以在实践的时候往往会这样设计 Actor-Critic。
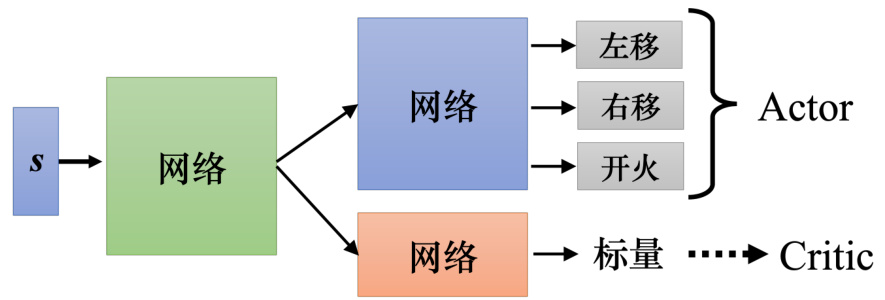
图 14.29 Actor-Critic 训练技巧
强化学习还可以直接用 Critic 决定要执行的动作,比如深度 Q 网络(Deep Q-Network,DQN)。DQN 有非常多的变形,有一篇非常知名的论文“Rainbow: Combining Improvementsin Deep Reinforcement Learning”[2],把 DQN 的七种变形集合起来,因为有七种变形集合起来,所以这个方法称为彩虹(rainbow)。
强化学习里面还有很多技巧,比如稀疏奖励的处理方法以及模仿学习,详细内容可参考《Easy RL:强化学习教程》[3],此处不再赘述。此外,视觉强化学习(Visual Reinforcement Learn-ing,VRL)是强化学习中非常有潜力的强化学习方向,与之前传统的基于状态的强化学习方法不同,其根据图片来直接学习控制策略,感兴趣的同学可阅读相关的论文,可参考 AwesomeVisual RL 论文清单:https://github.com/qiwang067/awesome-visual-rl。通过视觉强化学习能够玩我的世界(Minecraft)游戏,感兴趣的同学可参考 https://github.com/qiwang067/LS-Imagine。
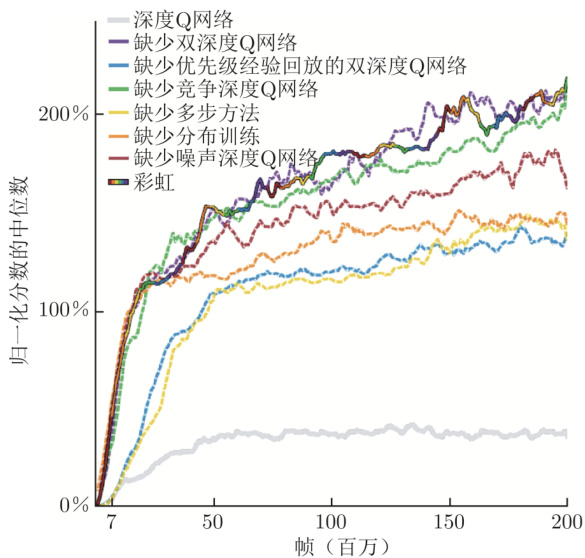
图 14.30 彩虹方法
参考文献
[1] SUTTON R S, BARTO A G. Reinforcement learning: An introduction(second edition) [M]. London:The MIT Press, 2018.
[2] HESSEL M, MODAYIL J, VAN HASSELT H, et al. Rainbow: Combining improvements in deep reinforcement learning[C]//Thirty-second AAAI conference on artificial intelligence. 2018.
[3] 王琦,杨毅远,江季. Easy RL:强化学习教程[M]. 北京: 人民邮电出版社, 2022.
